作為完賽的壓軸文章，首先要感謝學習路上夥伴們的幫助，其實在開始比賽時，小妹正在與 Rails 辛苦奮鬥中，會選擇單單以 Ruby 為主題的文章一方面是希望自己能夠有更紮實的基礎，同時藉著 Ruby 初階主題很容易就寫完而逼著自己去看一些進階讀物。

當然完賽並不只是一個句點，也可以當作下一段開始前的分號，未來的目標除了現在正在熟練中的 Rails 和 JavaScript 外，資料庫概念或者理論性的進階都在規劃中，所以我想以一個泛用的理論作為結尾。

時間複雜度(time complexity)

演算法由三個部分組成：輸入、計算步驟、輸出，我們通常希望它是明確的、有限的且有效率的，而通常判斷一個程式是否有效率有以下兩個依據：

1. 時間複雜度：完全地執行程式所需的計算機時間。
2. 空間複雜度：完全地執行程式所需的記憶體量。

然而，同一個程式運行的時間會隨著以下三種狀況而有所不同：

• 處理器：NASA 的超級電腦 vs 家用電腦。
• 數據量：只跑 1 筆數據 vs 10 萬筆數據。
• 數據形式：由小至大排列的數列 vs 由大至小排列的數列，兩者按大小排序。

若單以時間表示，並沒有一個標準化的依據，因此，時間複雜度其實是一種 步驟數依據數據量改變的變化趨勢 。

何謂依據數據量改變的變化趨勢呢？這裡舉個生活上的例子，假設手洗一件衣服加上扭乾只需要 5 分鐘，但洗衣機洗衣加上脫水至少需要 30 分鐘，當你出去旅行時，可能因為只有當天換洗衣物大多會選擇手洗，但日常生活動輒累積十幾件衣物就必定會想要有一台洗衣機了。

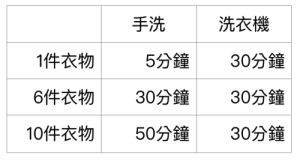
那麼我們如何表示時間複雜度呢？
一般來說會用 大寫 O 來表示，當有 n 個東西時會需要多少步驟達成？下圖列舉了許多常見的時間複雜度所畫出的函數圖：

1. O(1)
2. O(n)
3. O(log n)
4. O(nlogn)
5. O(n²)
6. O(2^n)

其中 Y 軸為步驟數， X 軸為資料個數。

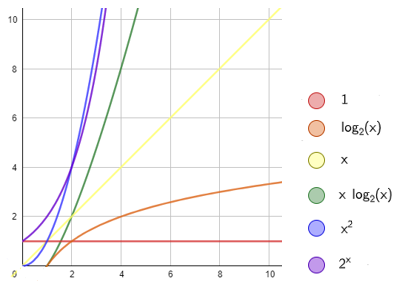
這裡的 X 就是 n ，可以發現在 n 不大時還各有優劣，但隨著 n 越來越大，差距也越來越可觀，通常我們會希望一個演算法至少能比 O(n²) 還要快，如果能到 O(n) 甚至是 O(log n) 的話是最為理想的。

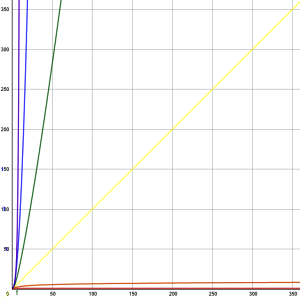
另外，其實大多數的時間複雜度都可以這六種表示，因為在數學上， n 非常大時，比較兩個數的大小可以只比較他們的首項(領導項)次方。因此在記錄時間複雜度時，我們同樣會只記錄最高次方的那一項。

那麼我們簡單介紹一下圖中這六種時間複雜度：

O(1)

例如陣列的讀取，當一個陣列被訂出來時，其中的每一個元素已帶有自己的 index ，所以「不論是找第幾個」，花費步驟都是 1 步。

O(n)

我們一樣用陣列來舉例，這裡的例子是搜尋，你是問它「那個誰是第幾個？」，這時電腦會從第一項開始逐項比對到匹配的目標，或許會有人有疑問：這樣只有正好要找的目標在最後一項才需要找 n 次啊！

但我們再分析一下，目標在第一項時需要 1 步，第二項需要 2 步，第 n 項就是 n 步，那麼相加起來就是 (1+n)*n/2 步，取每一項的機率又都是相當的，所以最後再除以 n 會得到 1/2(n+1)，領導項為 n。

O(logn)

最常見的例子為二分搜尋，就是小時候看的終極密碼，當要從 1 到 100 取得需要的數字時，一項一項找其實效率很差，如果每次都對半刪去，其實就是以 2 為底取對數個步驟就行了(注意這邊的log都是以 2 為底)。

O(nlogn)

最經典的例子就是合併排序( Merge Sort )，用文字非常難描述，所以就看影片吧！

O(n²)

個人最喜歡的例子就是 Bubble Sort，名字很可愛，也有一個可愛的影片可以輔助理解，當最大的數字在第一項時，第一輪( n-1 次比對)會換到最後一項，總共需要 n-1 輪，所以領導項為 n² 。

(00:55開始)

O(2^n)

通常我們會舉費波那契數列來當例子，是指在一串數字中，每一項是前兩項的和。數學上的定義為：
第 0 項 = 0
第 1 項 = 1
第 n 項 = 第 n-1 項 + 第 n-2 項
當要算出第 n 項實際的值時，都需要去找期前兩項，依此類推，每次都有 2 倍的步驟數。

在高中數學其實有一題延伸題型是「求得費波那契數列的一般式」，而它的結果為：

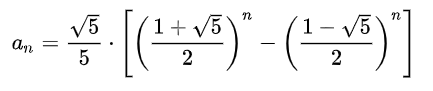
如此時間複雜度又會變回 O(1)，這也是幾世紀之前的人瘋狂需要將遞迴式轉換為一般式的原因，而程式語言的出現，好似表達了努力終究會勝過天分一般，只要交給電腦這種也許不會寫，但人人都看得懂的遞迴式，一樣能夠獲得成功的果實。

It does not matter how slowly you go so long as you do not stop. -- Andy Warhol 

此文同步刊登於CJ-Han的網站